Power Method on:
[Wikipedia]
[Google]
[Amazon]
In
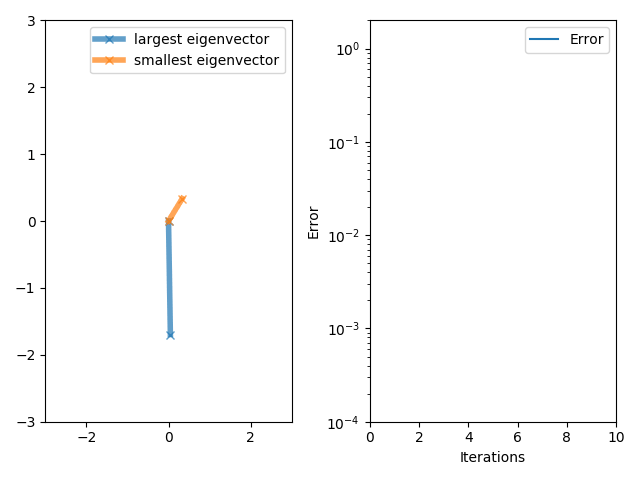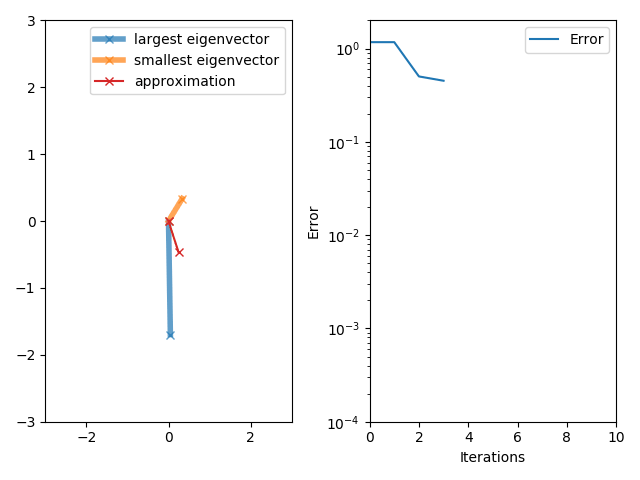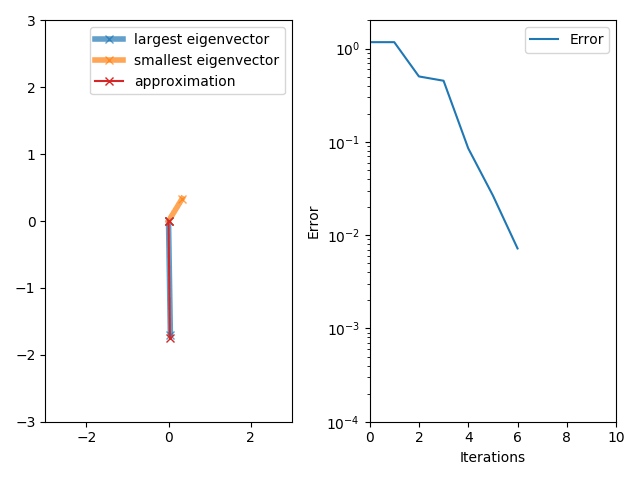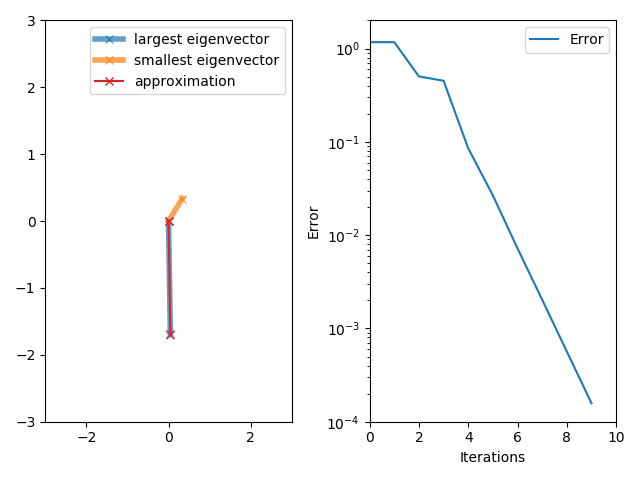 The power iteration algorithm starts with a vector , which may be an approximation to the dominant eigenvector or a random vector. The method is described by the
The power iteration algorithm starts with a vector , which may be an approximation to the dominant eigenvector or a random vector. The method is described by the
#!/usr/bin/env python3
import numpy as np
def power_iteration(A, num_iterations: int):
# Ideally choose a random vector
# To decrease the chance that our vector
# Is orthogonal to the eigenvector
b_k = np.random.rand(A.shape
for _ in range(num_iterations):
# calculate the matrix-by-vector product Ab
b_k1 = np.dot(A, b_k)
# calculate the norm
b_k1_norm = np.linalg.norm(b_k1)
# re normalize the vector
b_k = b_k1 / b_k1_norm
return b_k
power_iteration(np.array( 0.5, 0.5 .2, 0.8), 10)
The vector to an associated eigenvector. Ideally, one should use the
WTF: The who-to-follow system at Twitter
Proceedings of the 22nd international conference on World Wide Web The power iteration method is especially suitable for
mathematics
Mathematics is an area of knowledge that includes the topics of numbers, formulas and related structures, shapes and the spaces in which they are contained, and quantities and their changes. These topics are represented in modern mathematics ...
, power iteration (also known as the power method) is an eigenvalue algorithm
In numerical analysis, one of the most important problems is designing efficient and stable algorithms for finding the eigenvalues of a matrix. These eigenvalue algorithms may also find eigenvectors.
Eigenvalues and eigenvectors
Given an square ...
: given a diagonalizable
In linear algebra, a square matrix A is called diagonalizable or non-defective if it is similar to a diagonal matrix, i.e., if there exists an invertible matrix P and a diagonal matrix D such that or equivalently (Such D are not unique.) F ...
matrix
Matrix most commonly refers to:
* ''The Matrix'' (franchise), an American media franchise
** ''The Matrix'', a 1999 science-fiction action film
** "The Matrix", a fictional setting, a virtual reality environment, within ''The Matrix'' (franchis ...
, the algorithm will produce a number , which is the greatest (in absolute value) eigenvalue
In linear algebra, an eigenvector () or characteristic vector of a linear transformation is a nonzero vector that changes at most by a scalar factor when that linear transformation is applied to it. The corresponding eigenvalue, often denoted b ...
of , and a nonzero vector , which is a corresponding eigenvector
In linear algebra, an eigenvector () or characteristic vector of a linear transformation is a nonzero vector that changes at most by a scalar factor when that linear transformation is applied to it. The corresponding eigenvalue, often denoted b ...
of , that is, .
The algorithm is also known as the Von Mises iteration.Richard von Mises
Richard Edler von Mises (; 19 April 1883 – 14 July 1953) was an Austrian scientist and mathematician who worked on solid mechanics, fluid mechanics, aerodynamics, aeronautics, statistics and probability theory. He held the position of Gordo ...
and H. Pollaczek-Geiringer,
''Praktische Verfahren der Gleichungsauflösung'', ZAMM - Zeitschrift für Angewandte Mathematik und Mechanik 9, 152-164 (1929).
Power iteration is a very simple algorithm, but it may converge slowly. The most time-consuming operation of the algorithm is the multiplication of matrix by a vector, so it is effective for a very large sparse matrix
In numerical analysis and scientific computing, a sparse matrix or sparse array is a matrix in which most of the elements are zero. There is no strict definition regarding the proportion of zero-value elements for a matrix to qualify as sparse b ...
with appropriate implementation.
The method
 The power iteration algorithm starts with a vector , which may be an approximation to the dominant eigenvector or a random vector. The method is described by the
The power iteration algorithm starts with a vector , which may be an approximation to the dominant eigenvector or a random vector. The method is described by the recurrence relation
In mathematics, a recurrence relation is an equation according to which the nth term of a sequence of numbers is equal to some combination of the previous terms. Often, only k previous terms of the sequence appear in the equation, for a parameter ...
:
So, at every iteration, the vector is multiplied by the matrix and normalized.
If we assume has an eigenvalue that is strictly greater in magnitude than its other eigenvalues and the starting vector has a nonzero component in the direction of an eigenvector associated with the dominant eigenvalue, then a subsequence converges to an eigenvector associated with the dominant eigenvalue.
Without the two assumptions above, the sequence does not necessarily converge. In this sequence,
: ,
where is an eigenvector associated with the dominant eigenvalue, and . The presence of the term implies that does not converge unless . Under the two assumptions listed above, the sequence defined by
:
converges to the dominant eigenvalue (with Rayleigh quotient
In mathematics, the Rayleigh quotient () for a given complex Hermitian matrix ''M'' and nonzero vector ''x'' is defined as:
R(M,x) = .
For real matrices and vectors, the condition of being Hermitian reduces to that of being symmetric, and the co ...
).
One may compute this with the following algorithm (shown in Python with NumPy):
Rayleigh quotient
In mathematics, the Rayleigh quotient () for a given complex Hermitian matrix ''M'' and nonzero vector ''x'' is defined as:
R(M,x) = .
For real matrices and vectors, the condition of being Hermitian reduces to that of being symmetric, and the co ...
in order to get the associated eigenvalue.
This algorithm is used to calculate the ''Google PageRank
PageRank (PR) is an algorithm used by Google Search to rank web pages in their search engine results. It is named after both the term "web page" and co-founder Larry Page. PageRank is a way of measuring the importance of website pages. According ...
''.
The method can also be used to calculate the spectral radius
In mathematics, the spectral radius of a square matrix is the maximum of the absolute values of its eigenvalues. More generally, the spectral radius of a bounded linear operator is the supremum of the absolute values of the elements of its spectru ...
(the eigenvalue with the largest magnitude, for a square matrix) by computing the Rayleigh quotient
:
Analysis
Let be decomposed into itsJordan canonical form
In linear algebra, a Jordan normal form, also known as a Jordan canonical form (JCF),
is an upper triangular matrix of a particular form called a Jordan matrix representing a linear operator on a finite-dimensional vector space with respect to so ...
: , where the first column of is an eigenvector of corresponding to the dominant eigenvalue . Since the dominant eigenvalue of is unique, the first Jordan block of is the matrix where is the largest eigenvalue of ''A'' in magnitude. The starting vector can be written as a linear combination of the columns of ''V'':
:
By assumption, has a nonzero component in the direction of the dominant eigenvalue, so .
The computationally useful recurrence relation
In mathematics, a recurrence relation is an equation according to which the nth term of a sequence of numbers is equal to some combination of the previous terms. Often, only k previous terms of the sequence appear in the equation, for a parameter ...
for can be rewritten as:
:
where the expression: is more amenable to the following analysis.
:
The expression above simplifies as
:
The limit follows from the fact that the eigenvalue of is less than 1 in magnitude, so
:
It follows that:
:
Using this fact, can be written in a form that emphasizes its relationship with when ''k'' is large:
:
where and as
The sequence is bounded, so it contains a convergent subsequence. Note that the eigenvector corresponding to the dominant eigenvalue is only unique up to a scalar, so although the sequence may not converge,
is nearly an eigenvector of ''A'' for large ''k''.
Alternatively, if ''A'' is diagonalizable
In linear algebra, a square matrix A is called diagonalizable or non-defective if it is similar to a diagonal matrix, i.e., if there exists an invertible matrix P and a diagonal matrix D such that or equivalently (Such D are not unique.) F ...
, then the following proof yields the same result
Let λ1, λ2, ..., λ''m'' be the m eigenvalues (counted with multiplicity) of A and let ''v''1, ''v''2, ..., ''v''''m'' be the corresponding eigenvectors. Suppose that is the dominant eigenvalue, so that for .
The initial vector can be written:
:
If is chosen randomly (with uniform probability), then ''c''1 ≠ 0 with probability 1. Now,
:
On the other hand:
:
Therefore, converges to (a multiple of) the eigenvector . The convergence is geometric
Geometry (; ) is, with arithmetic, one of the oldest branches of mathematics. It is concerned with properties of space such as the distance, shape, size, and relative position of figures. A mathematician who works in the field of geometry is ca ...
, with ratio
:
where denotes the second dominant eigenvalue. Thus, the method converges slowly if there is an eigenvalue close in magnitude to the dominant eigenvalue.
Applications
Although the power iteration method approximates only one eigenvalue of a matrix, it remains useful for certaincomputational problem
In theoretical computer science, a computational problem is a problem that may be solved by an algorithm. For example, the problem of factoring
:"Given a positive integer ''n'', find a nontrivial prime factor of ''n''."
is a computational probl ...
s. For instance, Google
Google LLC () is an American multinational technology company focusing on search engine technology, online advertising, cloud computing, computer software, quantum computing, e-commerce, artificial intelligence, and consumer electronics. ...
uses it to calculate the PageRank
PageRank (PR) is an algorithm used by Google Search to rank web pages in their search engine results. It is named after both the term "web page" and co-founder Larry Page. PageRank is a way of measuring the importance of website pages. According ...
of documents in their search engine, and Twitter
Twitter is an online social media and social networking service owned and operated by American company Twitter, Inc., on which users post and interact with 280-character-long messages known as "tweets". Registered users can post, like, and ...
uses it to show users recommendations of whom to follow.Pankaj Gupta, Ashish Goel, Jimmy Lin, Aneesh Sharma, Dong Wang, and Reza Bosagh ZadeWTF: The who-to-follow system at Twitter
Proceedings of the 22nd international conference on World Wide Web The power iteration method is especially suitable for
sparse matrices
In numerical analysis and scientific computing, a sparse matrix or sparse array is a matrix in which most of the elements are zero. There is no strict definition regarding the proportion of zero-value elements for a matrix to qualify as sparse b ...
, such as the web matrix, or as the matrix-free method that does not require storing the coefficient matrix explicitly, but can instead access a function evaluating matrix-vector products . For non-symmetric matrices that are well-conditioned
In numerical analysis, the condition number of a function measures how much the output value of the function can change for a small change in the input argument. This is used to measure how sensitive a function is to changes or errors in the input ...
the power iteration method can outperform more complex Arnoldi iteration In numerical linear algebra, the Arnoldi iteration is an eigenvalue algorithm and an important example of an iterative method. Arnoldi finds an approximation to the eigenvalues and eigenvectors of general (possibly non-Hermitian) matrices by const ...
. For symmetric matrices, the power iteration method is rarely used, since its convergence speed can be easily increased without sacrificing the small cost per iteration; see, e.g., Lanczos iteration
The Lanczos algorithm is an iterative method devised by Cornelius Lanczos that is an adaptation of power methods to find the m "most useful" (tending towards extreme highest/lowest) eigenvalues and eigenvectors of an n \times n Hermitian matri ...
and LOBPCG Locally Optimal Block Preconditioned Conjugate Gradient (LOBPCG) is a matrix-free method for finding the largest (or smallest) eigenvalues and the corresponding eigenvectors of a symmetric generalized eigenvalue problem
:A x= \lambda B x,
for a ...
.
Some of the more advanced eigenvalue algorithms can be understood as variations of the power iteration. For instance, the inverse iteration In numerical analysis, inverse iteration (also known as the ''inverse power method'') is an Iterative method, iterative eigenvalue algorithm. It allows one to find an approximate
eigenvector when an approximation to a corresponding eigenvalue is alr ...
method applies power iteration to the matrix . Other algorithms look at the whole subspace generated by the vectors . This subspace is known as the Krylov subspace
In linear algebra, the order-''r'' Krylov subspace generated by an ''n''-by-''n'' matrix ''A'' and a vector ''b'' of dimension ''n'' is the linear subspace spanned by the images of ''b'' under the first ''r'' powers of ''A'' (starting from A^0=I), ...
. It can be computed by Arnoldi iteration In numerical linear algebra, the Arnoldi iteration is an eigenvalue algorithm and an important example of an iterative method. Arnoldi finds an approximation to the eigenvalues and eigenvectors of general (possibly non-Hermitian) matrices by const ...
or Lanczos iteration
The Lanczos algorithm is an iterative method devised by Cornelius Lanczos that is an adaptation of power methods to find the m "most useful" (tending towards extreme highest/lowest) eigenvalues and eigenvectors of an n \times n Hermitian matri ...
.
See also
*Rayleigh quotient iteration Rayleigh quotient iteration is an eigenvalue algorithm which extends the idea of the inverse iteration by using the Rayleigh quotient to obtain increasingly accurate eigenvalue estimates.
Rayleigh quotient iteration is an iterative method, that is, ...
* Inverse iteration In numerical analysis, inverse iteration (also known as the ''inverse power method'') is an Iterative method, iterative eigenvalue algorithm. It allows one to find an approximate
eigenvector when an approximation to a corresponding eigenvalue is alr ...
References
{{DEFAULTSORT:Power Iteration Numerical linear algebra Articles with example Python (programming language) code